QPS和并发数,究竟是何种关系?
一个开放性问题:
假设超市每分钟有10个人走出来,请估算超市里面有多少人?
是不是感觉手足无措呢?嗯,可能如此。其实,这个问题没有标准答案,关键还是考查思路。
我们先看一个有趣的定律,即Little’s Law,如下:
在一个稳定的系统中,设长时间观察到的平均顾客数量为L,长时间观察到的有效到达速率为λ,平均每个顾客在系统中花费的时间是W,则有如下关系式:
L = λW

Little’s Law的理解
假设有一水管,横截面积为2平方米,水速为5米/秒,即水的流量速度是10立方米/秒,很显然:
在长度100米的水管内,水量为200立方米,每滴水从流入到流出,耗时20秒,而水的流量速度是10立方米/秒。
也就是说,在这段水管中:
水量= 耗时 * 流量速度
这就是Little’s Law. 虽然很早就意识到了这一关系式,但毕业后才第一次听说Little’s Law.
Little’s Law的应用
Little’s Law模型很通用,因此,在很多场景中都能得到应用,比如工业界和计算机界,都会有意或无意用到该定律。
先看一个最好懂的例子:大一新生的招收速度是5000人/年,每个学生在大学停留4年,因此,整个大学的人数就是20000.
接下来,看看腾讯公司的一道笔试题目,简单但难倒不少人:
某互联网产品(例如,一款网络游戏)同时在线曲线(Average Concurrency Users,ACU)24小时数据如下图所示。
现已知全天平均在线人数为5000人,玩家每次登陆后平均在线时长为2小时。请你估计一下,平均每分钟约有多少玩家登录。
这个题目中的图是多余的,有误导性。很显然,根据Little’s Law,答案是42.
其中,ACU为平均同时在线人数,λ为平均每分钟登录的玩家数量,W为平均在线时长。
已知ACU为5000人,W为2小时(120分钟),代入公式得:
5000 = λ × 120
解方程得:λ ≈ 41.67
QPS和并发数的关系
在后台开发中,经常要涉及到QPS和并发数的概念。在很多场景下都需要进行压力测试,所以,有必要弄清它们之间的关系。
QPS和并发数的概念容易混淆,比如:1秒内并发地来了100个请求,这个100是QPS还是并发数? 来看看它们的含义:
QPS: 请求进入的速度
并发数: 系统中同时存在的请求数
根据Little’s Law,我们能得到如下的关系式:
并发数 = QPS * 耗时
以大学招生为例:大一新生的招收速度是5000人/年,每个学生在大学停留4年,整个大学的人数是20000,于是(下面的QPS改为以年为单位):
| QPS | 耗时 | 并发数 |
|---|---|---|
| 5000人/年 | 4年 | 20000人 |
以某公司为例:180000员工,必须早上8:30-9:00之间在考勤系统签到,每次签到在系统需要停留0.1秒,于是:
| QPS | 耗时 | 并发数 |
|---|---|---|
| 100人/秒 | 0.1秒 | 10人 |
以动物园为例:每秒有1个人进入动物园,每个人在动物园中停留2小时,于是:
| QPS | 耗时 | 并发数 |
|---|---|---|
| 1人/秒 | 2*3600秒 | 7200人 |
假设在理想情况下,某系统的请求进入速度是1亿次/秒,系统处理的时间趋近为0,那么这个系统的并发量是多少呢?很显然:
| QPS | 耗时 | 并发数 |
|---|---|---|
| 1亿次/秒 | 趋近0 | 趋近0次 |
可见,虽然每秒有1亿次请求,但在某一随机时刻观察系统,会发现系统中不存在请求堆积的问题,系统的并发数趋近0.这是一个高QPS、低延时系统,是一个很好的系统,轻轻松松地快速处理各种请求,来一个灭一个。值得一提的是,此时并发数很低,但这不表明系统实际能够承受的并发数很低,它实际上可能承受很高的并发数
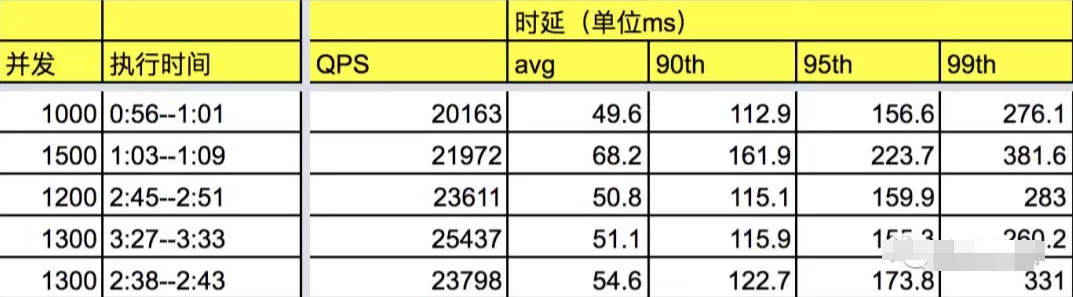
到此为止,应该清楚了QPS和并发数的关系,以后在开发或压测时,再也不会懵圈了。






